K Means
Dentro de los algoritmos de aprendizaje no supervisado en Machine Learning, uno de los más utilizados es K-Means. Este algoritmo es ampliamente empleado para la segmentación de clientes, detección de patrones y reducción de dimensionalidad.
K-Means funciona agrupando datos en K clusters basándose en su similitud, minimizando la distancia dentro de cada grupo. Aunque es eficiente y fácil de implementar, puede verse afectado por la elección inicial de los centroides y la forma de los datos.
En este artículo, exploraremos cómo funciona K-Means, sus ventajas y desventajas, y su implementación tanto en Python como en R.
¿Cómo funciona el algoritmo?
Este algoritmo opera de forma iterativa, repitiendo un conjunto de pasos hasta que los centroides converjan, es decir, hasta que sus posiciones dejen de cambiar significativamente entre iteraciones. Este proceso garantiza que los datos queden agrupados de manera óptima dentro de cada cluster.
-
Paso 1. Inicialización de centroides
Se eligen K centroides iniciales de manera aleatoria, estos pueden o no, ser puntos del dataset.
Paso 2. Asignación de los puntos a los clusters
Cada punto de datos se asigna al centroide más cercano utilizando una métrica de distancia (usualmente la distancia euclidiana).
Paso 3. Reubicación de centroides
Se recalculan los centroides como el promedio (de aquí el nombre K Means) de todos los puntos asignados a cada cluster.
Paso 4. Repetición hasta convergencia
Los pasos 2 y 3 se repiten hasta que los centroides dejen de moverse significativamente o se alcance el número máximo de iteraciones.
A continuación, encontrarás una aplicación interactiva que muestra el paso a paso del algoritmo KMeans.
Primero, seleccionamos los parámetros iniciales: la cantidad de observaciones que tendrá nuestro dataset de prueba, el grado de dispersión de los puntos con los que trabajaremos, y el número de clusters que esperamos obtener. Es importante recordar que, en este algoritmo, debemos conocer de antemano el número de clusters. Finalmente, se establece el parámetro de "semilla de aleatoriedad" o random state, que se utilizará para definir los centroides iniciales como para garantizar que los resultados sean reproducibles.Debajo del gráfico encontrarás un botón que te lleva a la siguiente iteración dentro del algoritmo, cuando este converja, la aplicación te lo hará saber y esto significará que se han encontrado los clusters finales.
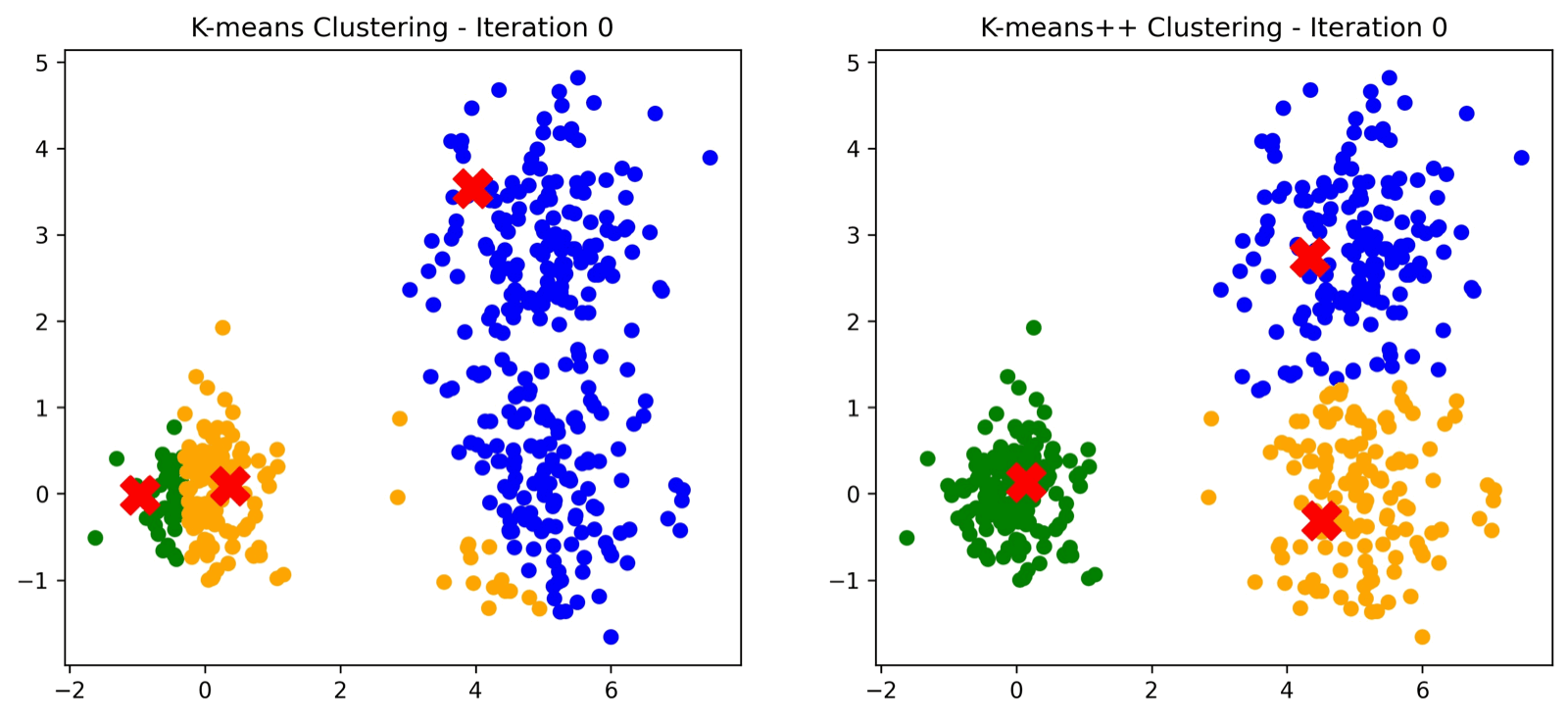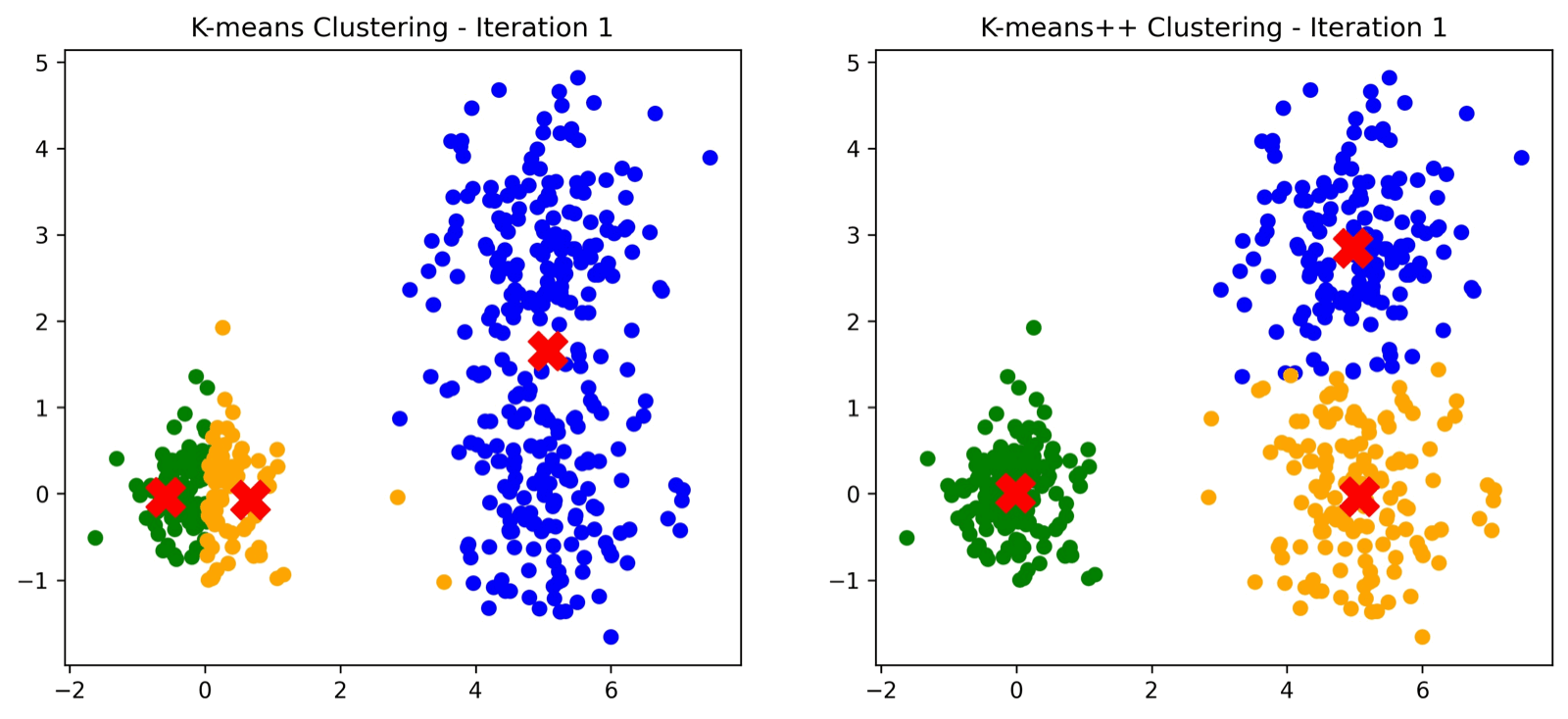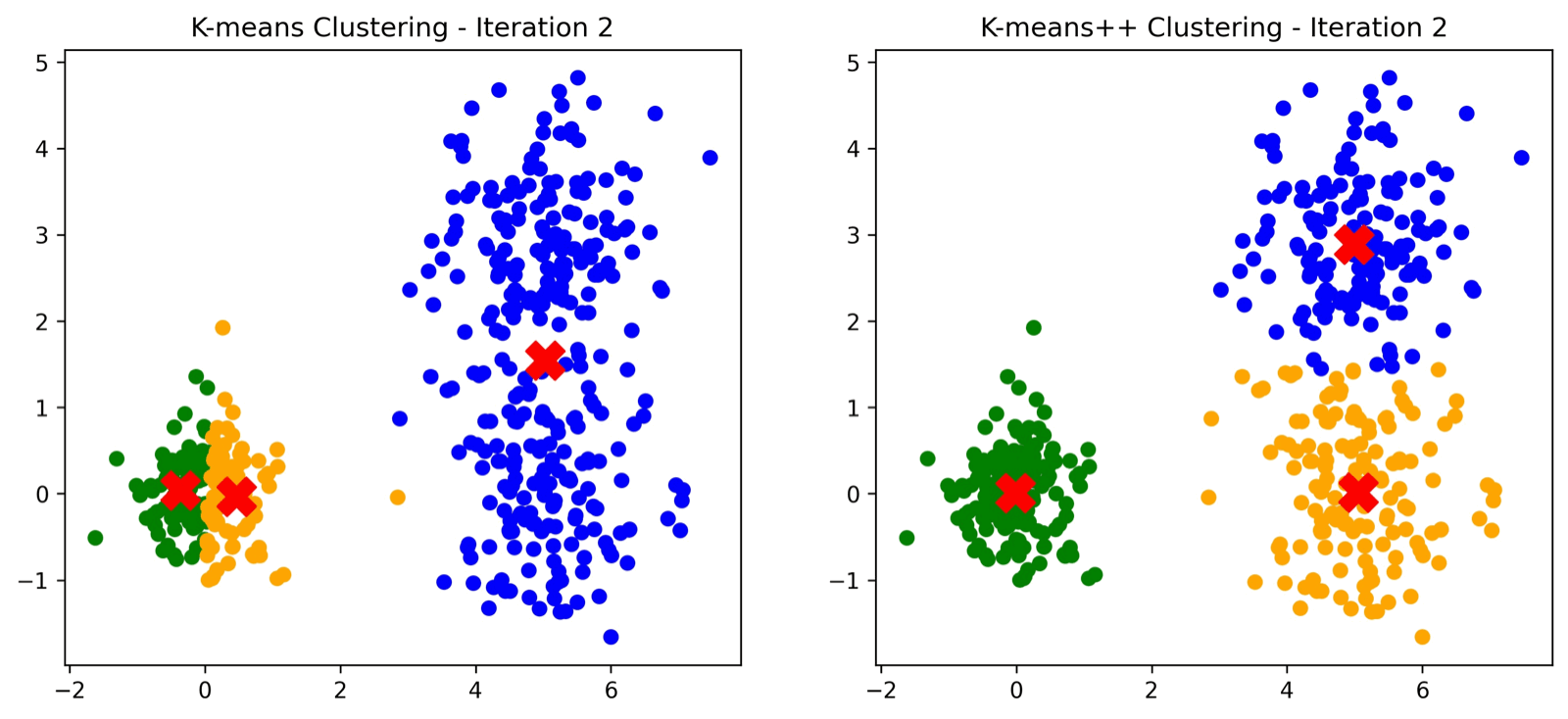
Del lado izquierdo el algoritmo tradicional de KMeans donde se incializan los centroides de manera aleatoria. Del lado derecho el algoritmo KMeans++ donde la inicialización de centroides asegura convergencia.
Tipos de distancias
KMeans es un algoritmo que, como se vió antes se basa en construir los clusters o segmentos tomando los puntos más cercanos a cada centroide. Sin embargo, el concepto de cercanía depende por completo de como se mida la distancia en espacio donde viven los puntos. A continuación hablaremos de algunas de las principales formas de medir distancia para este algoritmo.
- Distancia Euclideana
- Distancia Manhattan
- Distancia de Minkowski
La distancia euclidiana es la medida de distancia más utilizada en KMeans. Es simplemente la "distancia recta" entre dos puntos en un espacio multidimensional. Se calcula como la raíz cuadrada de la suma de las diferencias cuadradas entre las coordenadas de los puntos.
La distancia Manhattan mide la distancia total recorrida a lo largo de los ejes en una cuadrícula, es decir, la suma de las diferencias absolutas en las coordenadas de los puntos.
Generaliza tanto la distancia Euclidiana como la Manhattan. Dependiendo del valor de , se puede obtener la distancia Euclidiana (p=2) o la Manhattan (p=1).
Variación de KMeans: KMeans++
KMeans++ es una variación sobre el algoritmo clásico de KMeans que busca mejorar la selección de los centroides iniciales para evitar la convergencia a soluciones subóptimas. En el KMeans tradicional, los centroides iniciales se eligen de manera aleatoria, lo que puede llevar a que el algoritmo converja a una solución subóptima o tarde mucho en hacerlo, especialmente si los centroides iniciales están muy dispersos o cerca de puntos no representativos del dataset.
Esta manera de seleccionar los centroides iniciales tiene como objetivo maximizar la distancia entre los puntos seleccionados. Este procedimiento ayuda a que los centroides iniciales estén mejor distribuidos y, por lo tanto, el algoritmo converge más rápido y con mayor probabilidad de encontrar una mejor solución.
El proceso de selección de centroides en KMeans++ sigue estos pasos:
-
Paso 1. Selección del primer centroide
Se elige un punto aleatorio del dataset como el primer centroide.
Paso 2. Selección de los siguientes centroides
Se selecciona el siguiente centroide de entre los puntos, de tal forma que la probabilidad de elegir un punto como centroide sea directamente proporcional a su distancia desde el centroide más cercano previamente elegido. Es decir, se seleccionan como centroides iniciales puntos que están estratégicamente más alejados entre sí.
Paso 3. Iteración
Se repite el paso 2 hasta tener k centroides.
Paso 4. Ahora KMeans...
Con estos centroides, se procede con el algoritmo K-Means tradicional.
Ejemplo de implementación
from sklearn.cluster import KMeans
import numpy as np
# Generar datos de ejemplo
np.random.seed(42)
X = np.random.rand(100, 2) # 100 puntos con 2 características
# Configuración del modelo K-Means con todos los parámetros
kmeans = KMeans(
n_clusters=3, # Número de clusters
init='k-means++', # Inicialización ('random' o 'k-means++')
n_init=10, # Número de inicializaciones diferentes
max_iter=300, # Iteraciones máximas
tol=1e-4, # Tolerancia de convergencia
random_state=42, # Semilla para reproducibilidad
algorithm='lloyd', # Algoritmo ('lloyd', 'elkan')
)
# Ajustar modelo y obtener etiquetas
kmeans.fit(X)# Cargar paquete necesario
library(stats)
# Generar datos de ejemplo
set.seed(42)
X <- matrix(runif(200), ncol = 2) # 100 puntos con 2 características
# Aplicar K-Means con todos los parámetros disponibles
kmeans_result <- kmeans(
X,
centers = 3, # Número de clusters
iter.max = 300, # Iteraciones máximas
nstart = 10, # Número de reinicios
algorithm = "Lloyd" # Algoritmo ('Hartigan-Wong', 'Lloyd', 'Forgy', 'MacQueen')
)